-
Arithmetic expression을 Tree로 표현
Prefix - 연산자가 앞 ex) a+b -> +ab
Infix - 연산자가 중간 ex) a+b
Postfix - 연산자가 뒤 ex ) a+b -> ab+
Infix는 컴퓨터에서 Parsing이 어려워(Tiebreaker, Delimiter등 필요) Prefix나 Postfix로 표현함
Postfix로 표현했을 경우 식을 왼쪽부터 오른쪽으로 읽어나가며 피연산자는 stack에 저장, 이 후 연산자가 나오면 스택에서 피연산자를 꺼내 연산하면 됨
Infix를 Postfix로 바꾸려면 식을 왼쪽에서 오른쪽으로 읽어나가면서,
- 피연산자는 그대로 Postfix식에 적음
- ( 연산자는 연산자 stack에 push
- ) 연산자가 나오면 (가 나올 때 까지 stack에서 pop하여 Postfix식에 적음 (괄호는 Postfix식에 없음)
- 그 외 연산자들은 연산자 stack이 비어있으면 push하고 비어 있지 않으면, stack top 연산자와 읽은 연산자의 우선순위를 비교하여. (/와 *는 +와 -보다 우선순위가 높다.) 읽은 연산자가 top 연산자보다 우선순위가 높아질 때 까지 stack에서 연산자를 pop하여 Postfix식에 적고, 우선순위가 높아졌다면 읽은 연산자를 stack에 push한다.
- 식을 끝까지 다 읽었으면 stack에 남아있는 연산자들을 Postfix 식에 적는다.
Infix를 Prefix로 바꾸려면 오른쪽에서 왼쪽으로 읽으며 위와 같이 하고, 다시 식을 뒤집어주면 된다. https://www.geeksforgeeks.org/convert-infix-prefix-notation/
Convert Infix To Prefix Notation - GeeksforGeeks
While we use infix expressions in our day to day lives. Computers have trouble understanding this format because they need to keep in mind rules… Read More »
www.geeksforgeeks.org
Binary Tree
node 개수가 n인 Complete Binary Tree의 높이는 log n
높이가 h인 Complete Binary Tree의 node 개수는 2^h - 1
Tree 구현은 배열이나 Linked List 사용

배열을 통한 구현 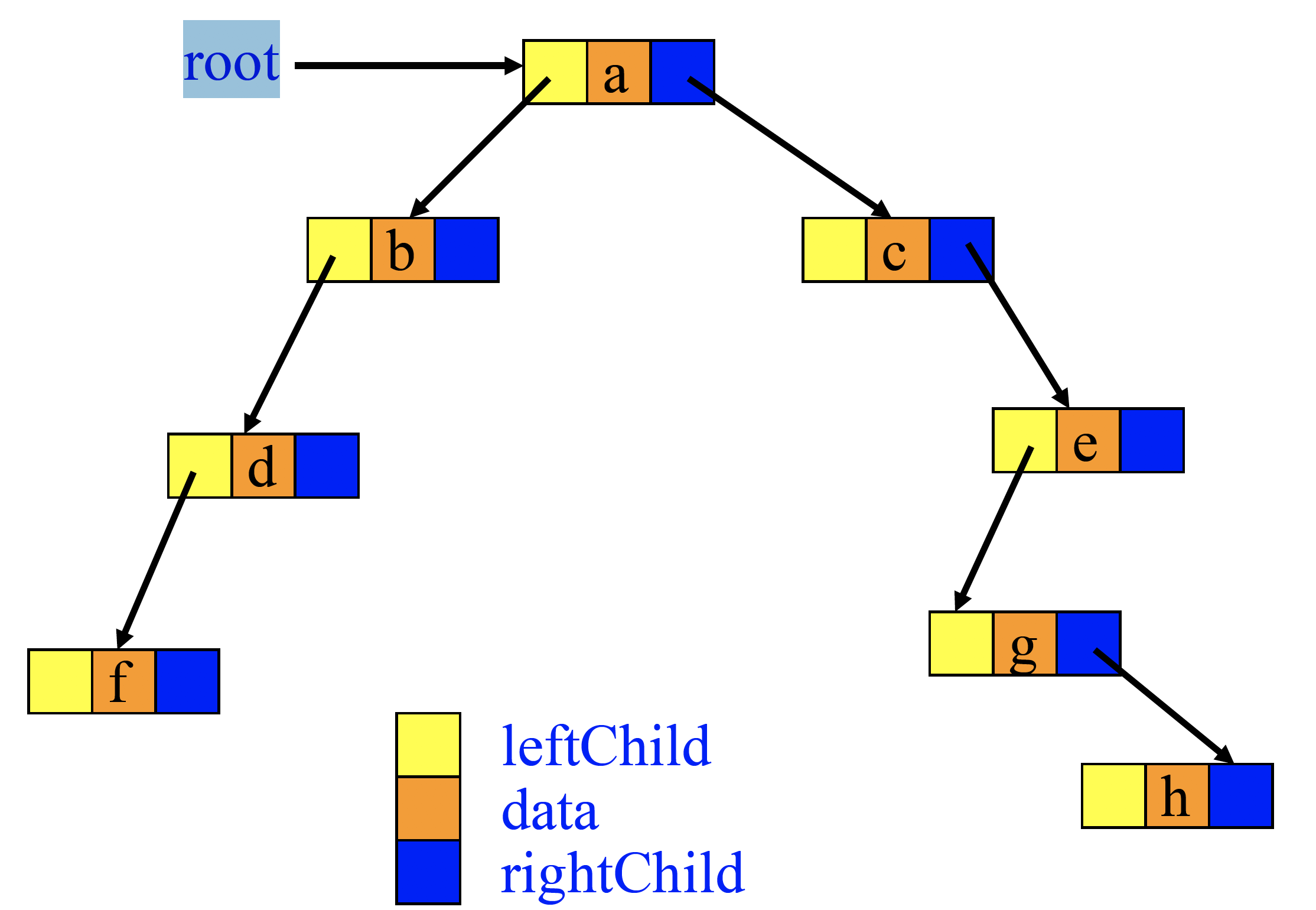
LinkedList를 통한 구현
Traversal Order
a
b c 일때
PreOrder a b c
void preOrder(treePointer ptr) { if (ptr != NULL) { visit(t); preOrder(ptr->leftChild); preOrder(ptr->rightChild); } }InOrder b a c
void inOrder(treePointer ptr) { if (ptr != NULL) { inOrder(ptr->leftChild); visit(ptr); inOrder(ptr->rightChild); } }PostOrder b c a
void postOrder(treePointer ptr) { if (ptr != NULL) { postOrder(ptr->leftChild); postOrder(ptr->rightChild); visit(t); } }LevelOrder a b c
Let ptr be a pointer to the tree root. while (ptr != NULL) { visit node pointed at by ptr and put its children on a FIFO queue; if FIFO queue is empty, set ptr = NULL; otherwise, delete a node from the FIFO queue and call it ptr; }PreOrder식과 PostOrder식, PreOrder식과 LevelOrder식, 또는 PostOrder식과 LevelOrder식으로 표현된 식 두개로 표현된 binary tree는 unique하지 않음.
ex)

두개의 식 쌍으로 두개의 tree가 표현됨 InOrder식과 PreOrder식, InOrder와 PostOrder, 또는 InOrder와 LevelOrder식 한 쌍이 하나의 Unique한 tree 표현 가능
'자료구조' 카테고리의 다른 글
Graph (0) 2019.09.03 Disjoint Sets (0) 2019.09.02 Selection Tree (0) 2019.09.02 Binary Search Tree (0) 2019.09.02 Priority Queue (0) 2019.09.02